들어가며

이 게시글을 시작으로 “알고리즘 풀자” 시리즈 (이하 알고풀자)를 적어보자 합니다.

저는 그냥 프로그래머 1에 지나지 않는 보통 사람입니다만, 다른 누군가에게 도움이 될 수 있겠죠?

게시글을 보시면서 오류가 있거나 이상한 부분이 있다면 언제든 알려주세요. (매너있는 지적 환영)

시작하겠습니다.

1. 알고리즘이란?

알고리즘은 어떠한 문제가 주어졌을 때, 그 문제를 해결하는 일련의 과정을 의미합니다.

예를 들어,

Example

민수는 여자친구와의 데이트 약속에 늦어서 최대한 빨리 약속 장소에 도착해야 합니다.

다음 3가지 방법으로 이동해야 합니다.

버스 + 지하철

도보 + 지하철

버스 + 도보

각 방법마다 소요시간이 주어질 때, 최대한 빨리 도착하는 방법을 선택하세요.

어떠신가요? 코드가 떠오르시나요? 중요한 점이 모든 케이스에 대한 코드는 같은 과정을 통해 정확한 답을 내야한다는 것입니다.

2. 알고리즘의 성능 표기 방법

만약 우리가 작성한 알고리즘 코드가 결과를 도출하는데 24시간이 걸린다면 문제가 있을겁니다. 이는 알고리즘 실행시간을 고려하지 않았기 때문인데요.

컴퓨터의 자원은 한정적이고 처리속도 역시 (언어, 컴파일러, 사양) 등 여러가지 요소에 의해 결정되기 때문입니다.

알고리즘이 한 줄씩 실행될 때마다 결과를 출력하기 위해 몇 번의 연산이 이루어지나, 즉 성장률이 나옵니다.

이러한 성장률을 점근적 표기법(Asymptotic Notation) 이라고 부릅니다.

점근적 표기법은 다음 세가지로 구분합니다.

최상의 경우 : 빅오메가 표기법 (Big-Ω)
평균의 경우 : 빅세타 표기법 (Big-θ)
최악의 경우 : 빅오 표기법 (Big-Ο)

평균으로 표기하면 가장 정확하고 좋겠지만, 평가하기가 까다롭습니다. 그래서 최악의 경우인 빅오를 사용하는데, 이는 알고리즘의 최악의 경우만 판단하여 평균과 가까운 성능으로 예측하기 쉽기때문입니다.

3. 빅오 표기법(Big-O)

빅오 표기법에는 시간 복잡도와 공간 복잡도가 있는데, 특수한 경우를 빼곤 시간 복잡도만 고려하면 됩니다.

현대의 메모리 발전에 따라 공간 복잡도의 중요도는 낮아졌습니다.

bigo
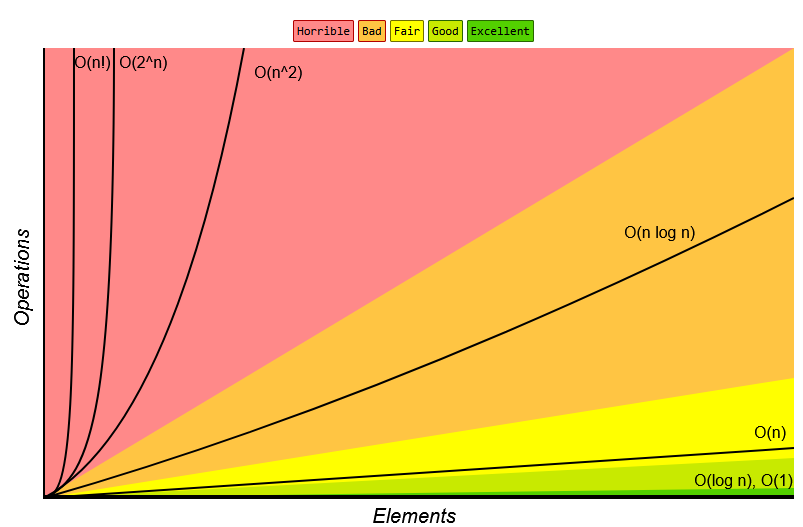
bigocheatsheet.com

시간 복잡도

시간 복잡도는 다른 말로 알고리즘의 성능입니다. 시간 복잡도가 상수 1에 가까울 수록 성능이 좋다는 의미이죠. 그렇다면 이 시간은 프로그램이 시작되고 종료될 때까지의 실행시간을 의미할까요?

아닙니다. 정확히는 알고리즘을 수행하기 위해 프로세스가 수행해야하는 연산을 수치화 한 것인데요. 이는 앞서 말했던 여러가지 변수(언어, 컴파일러, 사양)에 따라 편차가 달라지므로 명령어 수행횟수만 고려한답니다.

시간 복잡도를 볼 때 중요하게 보는 것은 N의 단위입니다. (N을 표기할 때는 계수와 상수 부분을 제외시킵니다.)

O(1) : 상수 시간
O(logN) : 로그 시간
O(N) : 선형 시간
O(N * LogN) : 선형 로그 시간
O(N^2) : 제곱 시간
O(2^N) : 지수 시간
O(N!) : 팩토리얼 시간
O(V+E) : 그래프 시간(특수)

이렇게 8가지로 나눌 수 있습니다.

그런데 실제 코딩 테스트 문제를 보면, 제한시간 1초 혹은 2초 이런식으로 표현되어 있는데, 이는 최대 데이터 수를 대입했을 때 연산이 1억번 이하로 마치게 되어야합니다.

왜 1억번이냐면 대부분의 현대 컴퓨터는 1초에 1억번의 연산 능력을 가지고 있습니다.

시간 복잡도 계산

제가 알고리즘에 대해 공부하면서 가장 신기했던게 ‘이건 로그N 만큼 걸리네’ , ‘이건 N만큼 걸리겠어’ 를 코드만 보고 바로 판단하는 부분이었습니다.

그래서 그 부분에 대해서 조금 팁을 드리고자 합니다. 물론 정확한건 계산을 해야되겠지만, 어느정도 유추할 수 있는 방법입니다.

O(1)

핵심 아이디어: 한 번의 실행으로 결과가 도출되는 알고리즘

상수 시간은 매우 쉬운 편입니다. 반복적으로 계산이 이루어지는 부분이 없다고 보시면 됩니다.

대표적인 예제:

int Sum(int a, int b)
{
    return a + b;
}

O(N)

핵심 아이디어: 인덱스 0 부터 N-1까지의 반복 한 번으로 결과가 도출되는 알고리즘

선형 시간은 범위가 주어지고 그 범위를 한 번만 순회해서 결과를 출력하는 방식입니다.

대표적인 예제:


int Solution(vector<int> Arr)
{
    int Sum = 0;
    for (int i = 0; i < Arr.size(); ++i) { // 인덱스 0부터 N-1까지 순회한다.
        Sum += Arr[i]; // Arr의 Index 값을 더해준다.
    }
    return Sum;
}

O(logN)

핵심 아이디어: 한 번 실행마다 탐색해야 할 범위가 절반(또는 일정한 비율)으로 줄어드는 알고리즘

로그 시간은 순회마다 범위가 절반으로 줄어드는 방식입니다.

대표적인 예제:

bool BinarySearch(const vector<int>& arr, int target)
{
    int left = 0;
    int right = arr.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2; // 중간 지점
        if (arr[mid] == target) {
            return true;
        }
        
        // 중간값이 타겟보다 작으면, 왼쪽 절반을 버린다.
        if (arr[mid] < target) {
            left = mid + 1;
        } 
        // 중간값이 타겟보다 크면, 오른쪽 절반을 버린다.
        else {
            right = mid - 1;
        }
    }
    // while 루프가 한 번 돌 때마다 탐색 범위가 절반으로 줄어듭니다.
    // N개의 원소를 전부 탐색하는 게 아니라, log₂(N)번 만에 탐색이 끝납니다.
    return false;
}

O(N * LogN)

핵심 아이디어: O(N)번 반복하는데, 반복문 안에서 O(logN)의 작업을 수행하는 알고리즘

선형 로그 시간은 선형 시간과 로그 시간을 합친 알고리즘으로, N명의 학생을 키 순서대로 줄 세운다고 했을 때 이미 정렬된 줄의 어디에 들어가야 할지 빠르게 찾아야 합니다. 이 ‘빠르게 찾는 과정’이 앞 선 이진 탐색과 비슷한 O(logN) 이고, N명의 학생에 대해 반복하므로 O(N * LogN)이 걸립니다.

void Sort(vector<int>& arr)
{
    for (int i = 0; i < n; ++i)
    {
        BinarySearch(...);
    }
}

O(2^n)

핵심 아이디어: 입력 N개에 대해 각각의 요소가 두 가지(혹은 그 이상) 선택지를 가지고 있고, 가능한 모든 조합을 탐색하는 알고리즘

지수 시간은 N개의 재료가 있을 때, 만들 수 있는 모든 피자 조합을 구하는 것과 같습니다. 각 재료마다 ‘넣는다’ 또는 ‘안넣는다’ 2가지 선택지가 있죠. 재료가 N개면 총 2 x 2 x … x 2 (N번) 2^N 가지 조합이 나옵니다.

// 집합의 모든 부분집합을 구하는 재귀 함수
// n개의 원소가 있을 때, 각 원소를 포함하거나/포함하지 않거나 2가지 선택이 존재합니다.
void generateSubsets(int k, int n, vector<int>& current_subset) 
{
    if (k == n) {
        // 하나의 부분집합 완성
        return;
    }

    // 1. k번째 원소를 포함하지 않는 경우
    generateSubsets(k + 1, n, current_subset);

    // 2. k번째 원소를 포함하는 경우
    current_subset.push_back(k);
    generateSubsets(k + 1, n, current_subset);
    current_subset.pop_back();
}

O(V+E)

핵심 아이디어: V(정점) 와 E(간선)로 이루어진 그래프 자료구조를 탐색할 때 사용되는 알고리즘

그래프 시간은 모든 정점을 한 번씩 방문하고, 모든 간선을 한 번씩 검사하는 방법입니다.

// 인접 리스트로 그래프가 주어졌을 때의 BFS
void bfs(int start_node, int V, const vector<vector<int>>& adj) 
{
    vector<bool> visited(V + 1, false);
    queue<int> q;

    q.push(start_node);
    visited[start_node] = true;

    // 큐가 빌 때까지 반복 -> 모든 정점은 최대 한 번만 큐에 들어갑니다. (V번)
    while (!q.empty()) {
        int u = q.front();
        q.pop();

        // 현재 정점과 연결된 모든 간선을 검사합니다.
        // 이 for문은 알고리즘 전체를 통틀어 모든 간선의 수(E)만큼 실행됩니다.
        for (int v : adj[u]) {
            if (!visited[v]) {
                visited[v] = true;
                q.push(v);
            }
        }
    }
}

마무리

이렇게 첫 시리즈 게시물이 끝났습니다. 시간 복잡도에 대해 조금 알게되셨나요? 마지막 계산 부분에서 다루지 않은 시간 복잡도 역시 개인적으로 찾아보셨으면 좋겠습니다. 감사합니다.

#BigO #General

(알고풀자) 1. 시간 복잡도

들어가며

1. 알고리즘이란?

2. 알고리즘의 성능 표기 방법

3. 빅오 표기법(Big-O)

시간 복잡도

시간 복잡도 계산

O(1)

O(N)

O(logN)

O(N * LogN)

O(2^n)

O(V+E)

마무리